A certain class of surfaces in space, known as quadric surfaces, can be defined with the
general polynomial of two variables:
\(Ax^2+By^2+Cxy+Dx+Ey+F=0.\)
Such an equation can look somewhat intimidating, Our interest isn't in understanding the equation, but in understanding the surfaces they define. It turns out that the six most important quadric surfaces are the paraboloid, the ellipsoid, the elliptic cone, the hyperboloids of one and two sheets, and the hyperbolic paraboloid (pictured above).
One of the great features of the quadric sections is that their cross sections are conic sections. It is neat to see how "stacking" certain conics together, "side-by-side", creates an interesting surface.
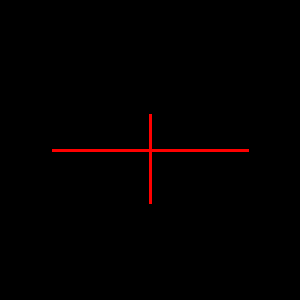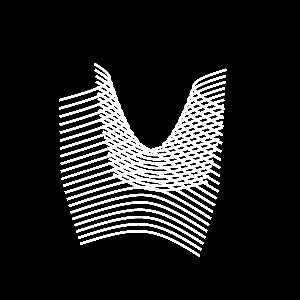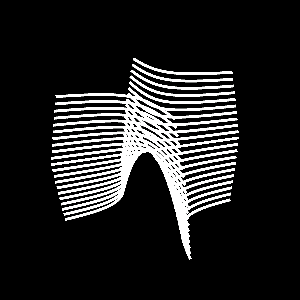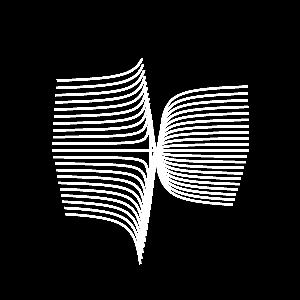
Above, a series of parabolas, all facing down but with different vertical shifts, are placed together, forming the hyperbolic paraboloid (it looks like a Pringles® chip.)
One can also form a hyperbolic paraboloid by placing up facing parabolas side by side, again with different vertical shifts. That is demonstrated below. The gif following that shows the hyperbolic paraboloid being formed by both sets of parabolas; that graphic takes some time to comprehend though the final surface looks great. Right at the "middle" there is the intersection of an up and down facing parabola, which creates a saddle point.
One can also form a hyperbolic paraboloid by placing up facing parabolas side by side, again with different vertical shifts. That is demonstrated below. The gif following that shows the hyperbolic paraboloid being formed by both sets of parabolas; that graphic takes some time to comprehend though the final surface looks great. Right at the "middle" there is the intersection of an up and down facing parabola, which creates a saddle point.
One can create a hyperbolic paraboloid with more than just parabolas; one can create a hyperbolic paraboloid by placing hyperbolas side by side. In this case, we stack them vertically, as shown below.
It is important to note that all of the hyperbolic paraboloids shown above are the same; they are just drawn using different cross sections.
An ellipsoid, no matter how you slice it, is made up of ellipses. Two different sets of slices are shown immediately below, followed by those slices put together.
The final quadric surface we demonstrate is the elliptic cone. Given its name, it is not surprising to find out that stacking ellipses on top of each other in the right manner creates a double-napped cone.
We leave it to the reader to figure out what the other cross sections look like.
Consider following us on Twitter; we'll tweet only when a new post is up.







No comments:
Post a Comment